For time-resolved simulations, you may want to save a dynamic (animated) plot as a video so that it can be played back in sync with other simulation variables. This guide describes how to accomplish this with the “double pendulum simulation” as an example.

Nominal has 1st class support for video ingestion, analysis, time sychronization across sensor channels, and automated checks that signal when a video feature is out-of-spec.

This guide demonstrates how to upload a video file to Nominal in Python. Other guides in the Video section demonstrate basic Python video analysis and computer vision for video pre-processing prior to Nominal upload.

Double pendulum simulation

The double pendulum consists of two pendulums attached end to end, where the motion of one pendulum influences the other, creating complex, chaotic dynamics. It is a classic problem in physics that demonstrates how even simple systems can exhibit unpredictable behavior due to sensitivity to initial conditions.

If you’ve never seen the double pendulum simulation, below is a time-resolved animation of its solution. Note that the simulation length is 25 seconds.

1 import numpy as np
2 import plotly.graph_objs as go
3 from scipy.integrate import solve_ivp
4 
5 # Parameters for the double pendulum
6 m1, m2 = 1.0, 1.0       # masses of the pendulums
7 L1, L2 = 1.0, 1.0       # lengths of the pendulums
8 g = 9.81                # gravitational acceleration
9 
10 # Equations of motion for the double pendulum
11 def double_pendulum_equations(t, y):
12     theta1, z1, theta2, z2 = y
13     delta = theta2 - theta1
14 
15     # Equations of motion
16     den1 = (m1 + m2) * L1 - m2 * L1 * np.cos(delta) * np.cos(delta)
17     den2 = (L2 / L1) * den1
18 
19     dydt = [
20         z1,
21         (m2 * L1 * z1 * z1 * np.sin(delta) * np.cos(delta) +
22          m2 * g * np.sin(theta2) * np.cos(delta) +
23          m2 * L2 * z2 * z2 * np.sin(delta) -
24          (m1 + m2) * g * np.sin(theta1)) / den1,
25         z2,
26         (- m2 * L2 * z2 * z2 * np.sin(delta) * np.cos(delta) +
27          (m1 + m2) * (g * np.sin(theta1) * np.cos(delta) -
28                       L1 * z1 * z1 * np.sin(delta) -
29                       g * np.sin(theta2))) / den2
30     ]
31     return dydt
32 
33 # Initial conditions and time span
34 y0 = [np.pi / 2, 0, np.pi / 2, 0]  # initial angles and angular velocities
35 t_span = (0, 25)
36 t_eval = np.linspace(*t_span, 500)
37 
38 # Solve the equations
39 solution = solve_ivp(double_pendulum_equations, t_span, y0, t_eval=t_eval, method='RK45')
40 theta1, theta2 = solution.y[0], solution.y[2]
41 
42 # Calculate positions of the pendulums
43 x1 = L1 * np.sin(theta1)
44 y1 = -L1 * np.cos(theta1)
45 x2 = x1 + L2 * np.sin(theta2)
46 y2 = y1 - L2 * np.cos(theta2)
47 
48 # Create animation using plotly
49 frames = []
50 for i in range(len(t_eval)):
51     frames.append(go.Frame(data=[
52         go.Scatter(x=[0, x1[i], x2[i]], y=[0, y1[i], y2[i]], mode="lines+markers")
53     ]))
54 
55 # Set up the initial plot
56 fig = go.Figure(
57     data=[go.Scatter(x=[0, x1[0], x2[0]], y=[0, y1[0], y2[0]], mode="lines+markers")],
58     layout=go.Layout(
59         title="Double Pendulum Animation",
60         xaxis=dict(range=[-2, 2], zeroline=False),
61         yaxis=dict(range=[-2, 2], zeroline=False),
62         updatemenus=[dict(type="buttons", showactive=False, buttons=[dict(label="Play",
63                                                                           method="animate",
64                                                                           args=[None, {"frame": {"duration": 50, "redraw": True},
65                                                                                        "fromcurrent": True}])])],
66         width=600,
67         height=600
68     ),
69     frames=frames
70 )
71 
72 # Show the animation
73 fig.show()

Convert animation to video

To convert the Plotly animation to a video, we’ll install the imagio library with the ffmpeg plugin:

pip3 install imageio[ffmpeg]

Prior to running the above command, you’ll also want to install the underlying ffmpeg library. On a Mac you can install this with brew install ffmpeg. For installation instructions for other operating systems, please see the official FFmpeg download page.

For more information about this plugin, please refer to the imageio docs.

Now, we’ll modify the simulation code above to to save an image for each animation frame with Plotly’s write_image() function. At the end of the simulation, we’ll stitch these images together into a video with imageio’s get_writer() function.

1 import os
2 import numpy as np
3 import plotly.graph_objs as go
4 from scipy.integrate import solve_ivp
5 import imageio.v2 as imageio
6 
7 # Parameters for the double pendulum
8 m1, m2 = 1.0, 1.0
9 L1, L2 = 1.0, 1.0
10 g = 9.81
11 
12 # Equations of motion
13 def double_pendulum_equations(t, y):
14     theta1, z1, theta2, z2 = y
15     delta = theta2 - theta1
16 
17     den1 = (m1 + m2) * L1 - m2 * L1 * np.cos(delta) ** 2
18     den2 = (L2 / L1) * den1
19 
20     dydt = [
21         z1,
22         (m2 * L1 * z1 ** 2 * np.sin(delta) * np.cos(delta) +
23          m2 * g * np.sin(theta2) * np.cos(delta) +
24          m2 * L2 * z2 ** 2 * np.sin(delta) -
25          (m1 + m2) * g * np.sin(theta1)) / den1,
26         z2,
27         (- m2 * L2 * z2 ** 2 * np.sin(delta) * np.cos(delta) +
28          (m1 + m2) * (g * np.sin(theta1) * np.cos(delta) -
29                       L1 * z1 ** 2 * np.sin(delta) -
30                       g * np.sin(theta2))) / den2
31     ]
32     return dydt
33 
34 # Initial conditions and time span
35 y0 = [np.pi / 2, 0, np.pi / 2, 0]
36 t_span = (0, 25)
37 t_eval = np.linspace(*t_span, 500)
38 
39 # Solve the equations
40 solution = solve_ivp(double_pendulum_equations, t_span, y0, t_eval=t_eval, method='RK45')
41 theta1, theta2 = solution.y[0], solution.y[2]
42 
43 # Calculate positions
44 x1 = L1 * np.sin(theta1)
45 y1 = -L1 * np.cos(theta1)
46 x2 = x1 + L2 * np.sin(theta2)
47 y2 = y1 - L2 * np.cos(theta2)
48 
49 # Save frames as images
50 filenames = []
51 for i in range(len(t_eval)):
52     fig = go.Figure(
53         data=[go.Scatter(x=[0, x1[i], x2[i]], y=[0, y1[i], y2[i]], mode="lines+markers")],
54         layout=go.Layout(
55             title="Double Pendulum Animation",
56             xaxis=dict(range=[-2, 2], zeroline=False),
57             yaxis=dict(range=[-2, 2], zeroline=False),
58             width=600,
59             height=600
60         )
61     )
62     filename = f'frame_{i:03d}.png'
63     fig.write_image(filename)
64     filenames.append(filename)
65 
66 # Create video from frames using imageio
67 with imageio.get_writer('double_pendulum.mp4', fps=20) as writer:
68     for filename in filenames:
69         image = imageio.imread(filename)
70         writer.append_data(image)
71 
72 # Cleanup
73 for filename in filenames:
74     os.remove(filename)
75 
76 print("Video saved as 'double_pendulum.mp4'")

Note that the simulation video has been saved to double_pendulum.mp4.

Display video inline

If you’re working in Jupyter notebook, here’s a shortcut to display the video inline in your notebook.

1 from ipywidgets import Video
2 Video.from_file(video_path)

Save simulation channels

We’ll run the same simulation a final time to extract channels such as the pendulum fulcrum’s heights, momentums, PEs and KEs, etc.

Simulations are often time-consuming to run. In practice, you would want to extract the simulation result, video frames, and important channel values in a single pass. For the pedagogical purposes of this tutorial, however, we’ve separated the extraction of these 3 artifacts into 3 identical but separate simulation runs.

1 import numpy as np
2 import pandas as pd
3 from scipy.integrate import solve_ivp
4 from datetime import datetime, timedelta
5 
6 # Parameters for the double pendulum
7 m1, m2 = 1.0, 1.0       # masses of the pendulums
8 L1, L2 = 1.0, 1.0       # lengths of the pendulums
9 g = 9.81                # gravitational acceleration
10 
11 # Equations of motion for the double pendulum
12 def double_pendulum_equations(t, y):
13     theta1, z1, theta2, z2 = y
14     delta = theta2 - theta1
15 
16     # Equations of motion
17     den1 = (m1 + m2) * L1 - m2 * L1 * np.cos(delta) * np.cos(delta)
18     den2 = (L2 / L1) * den1
19 
20     dydt = [
21         z1,
22         (m2 * L1 * z1 * z1 * np.sin(delta) * np.cos(delta) +
23          m2 * g * np.sin(theta2) * np.cos(delta) +
24          m2 * L2 * z2 * z2 * np.sin(delta) -
25          (m1 + m2) * g * np.sin(theta1)) / den1,
26         z2,
27         (- m2 * L2 * z2 * z2 * np.sin(delta) * np.cos(delta) +
28          (m1 + m2) * (g * np.sin(theta1) * np.cos(delta) -
29                       L1 * z1 * z1 * np.sin(delta) -
30                       g * np.sin(theta2))) / den2
31     ]
32     return dydt
33 
34 # Initial conditions and time span
35 y0 = [np.pi / 2, 0, np.pi / 2, 0]  # initial angles and angular velocities
36 t_span = (0, 25)
37 t_eval = np.linspace(*t_span, 500)
38 
39 # Solve the equations
40 solution = solve_ivp(double_pendulum_equations, t_span, y0, t_eval=t_eval, method='RK45')
41 theta1, theta2 = solution.y[0], solution.y[2]
42 
43 # Calculate positions, velocities, accelerations, and energies
44 x1 = L1 * np.sin(theta1)
45 y1 = -L1 * np.cos(theta1)
46 x2 = x1 + L2 * np.sin(theta2)
47 y2 = y1 - L2 * np.cos(theta2)
48 
49 vx1 = np.gradient(x1, t_eval)
50 vy1 = np.gradient(y1, t_eval)
51 vx2 = np.gradient(x2, t_eval)
52 vy2 = np.gradient(y2, t_eval)
53 
54 ax1 = np.gradient(vx1, t_eval)
55 ay1 = np.gradient(vy1, t_eval)
56 ax2 = np.gradient(vx2, t_eval)
57 ay2 = np.gradient(vy2, t_eval)
58 
59 momentum_1_x = m1 * vx1
60 momentum_1_y = m1 * vy1
61 momentum_2_x = m2 * vx2
62 momentum_2_y = m2 * vy2
63 
64 height_1 = y1 + L1 + L2
65 height_2 = y2 + L1 + L2
66 
67 kinetic_energy_1 = 0.5 * m1 * (vx1**2 + vy1**2)
68 kinetic_energy_2 = 0.5 * m2 * (vx2**2 + vy2**2)
69 
70 potential_energy_1 = m1 * g * (y1 + L1 + L2)
71 potential_energy_2 = m2 * g * (y2 + L1 + L2)
72 
73 # Generate ISO8601 formatted timestamps
74 start_time = datetime.now()
75 absolute_time = [start_time + timedelta(seconds=t) for t in t_eval]
76 
77 # Create DataFrame with full header names
78 data = {
79     "Timestamp (ISO8601)": [t.isoformat() for t in absolute_time],
80     "Momentum 1 (X)": momentum_1_x, "Momentum 1 (Y)": momentum_1_y,
81     "Momentum 2 (X)": momentum_2_x, "Momentum 2 (Y)": momentum_2_y,
82     "Acceleration 1 (X)": ax1, "Acceleration 1 (Y)": ay1,
83     "Acceleration 2 (X)": ax2, "Acceleration 2 (Y)": ay2,
84     "Velocity 1 (X)": vx1, "Velocity 1 (Y)": vy1,
85     "Velocity 2 (X)": vx2, "Velocity 2 (Y)": vy2,
86     "Height 1": height_1, "Height 2": height_2,
87     "Kinetic Energy 1": kinetic_energy_1, "Kinetic Energy 2": kinetic_energy_2,
88     "Potential Energy 1": potential_energy_1, "Potential Energy 2": potential_energy_2
89 }
90 
91 df = pd.DataFrame(data)
92 
93 # Save the DataFrame to a CSV file
94 csv_file_path_full_headers = "double_pendulum_full_headers.csv"
95 df.to_csv(csv_file_path_full_headers, index=False)
96 
97 df

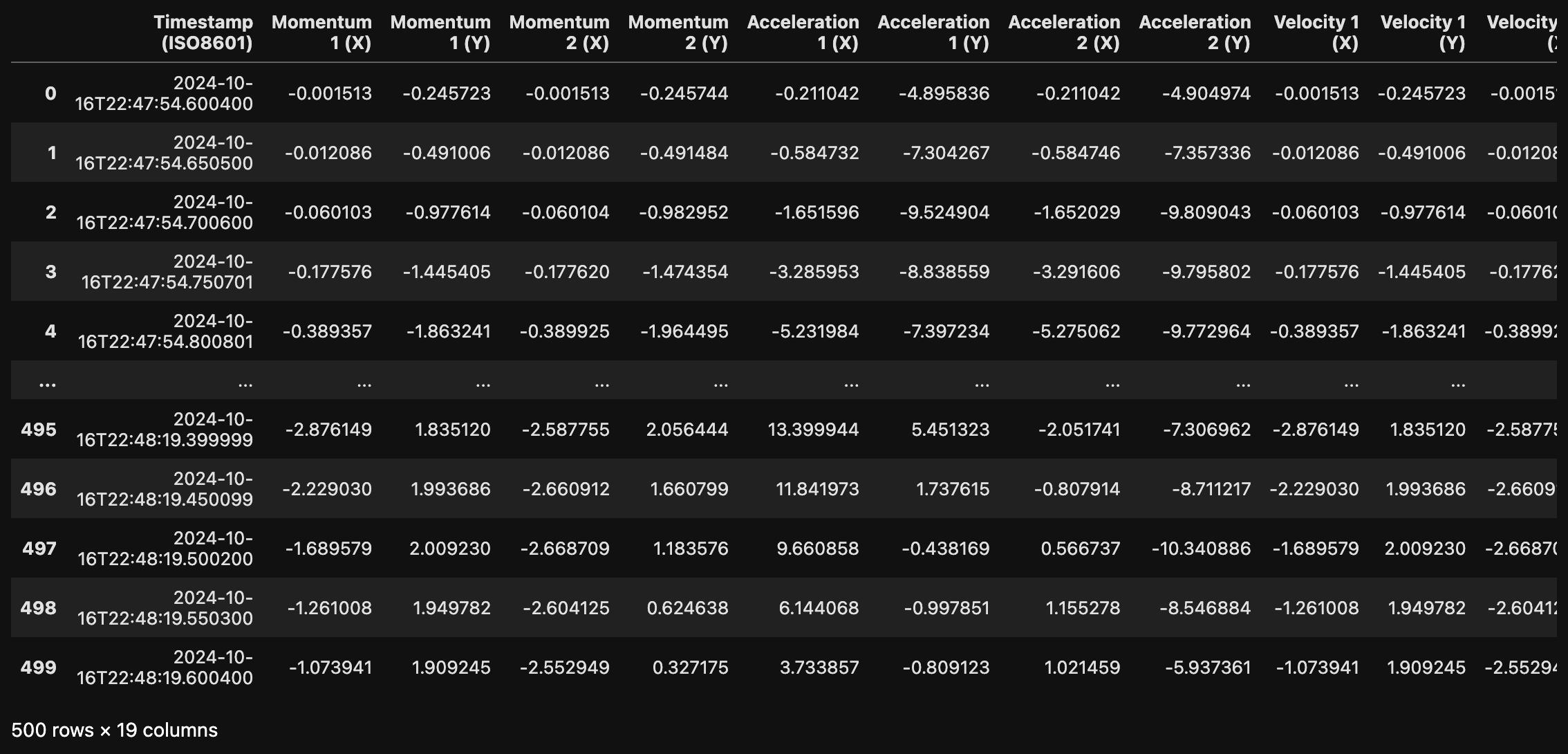
Note that we saved the channel data in a CSV file - double_pendulum_full_headers.csv.

Finally, let’s upload these channels and video to Nominal so that we can visualize them together.

Connect to Nominal

Get your Nominal API token from your User settings page.

See the Quickstart for more details on connecting to Nominal from Python.

1 import nominal.nominal as nm
2 
3 nm.set_token(
4     base_url = 'https://api.gov.nominal.io/api',
5     token = '* * *' # Replace with your Access Token from 
6                     # https://app.gov.nominal.io/settings/user?tab=tokens
7 )

If you’re not sure whether your company has a Nominal tenant, please reach out to us.

Create a Run

First, we’ll create a Run to which we’ll attach our video and channel data.

In Nominal, Runs are containers of multimodal test data - including Datasets, Videos, Logs, and database connections.

To see your organization’s latest Runs, head over to the Runs page

1 import nominal.nominal as nm
2 
3 sim_run = nm.create_run_csv(
4     file = "double_pendulum_full_headers.csv",
5     name = "double_pendulum_run",
6     timestamp_column = "Timestamp (ISO8601)",
7     timestamp_type = "iso_8601",
8 )

Note that create_run_csv() automatically adds the CSV file to the Run and sets the Run’s start and end time.

Add Video to Run

Nominal Video uploads need an absolute start time. We’ll grab this start time from the channel dataframe:

1 ts_start = df['Timestamp (ISO8601)'][0]
2 ts_start

2024-10-16T22:47:54.600400

Adjust Video Start

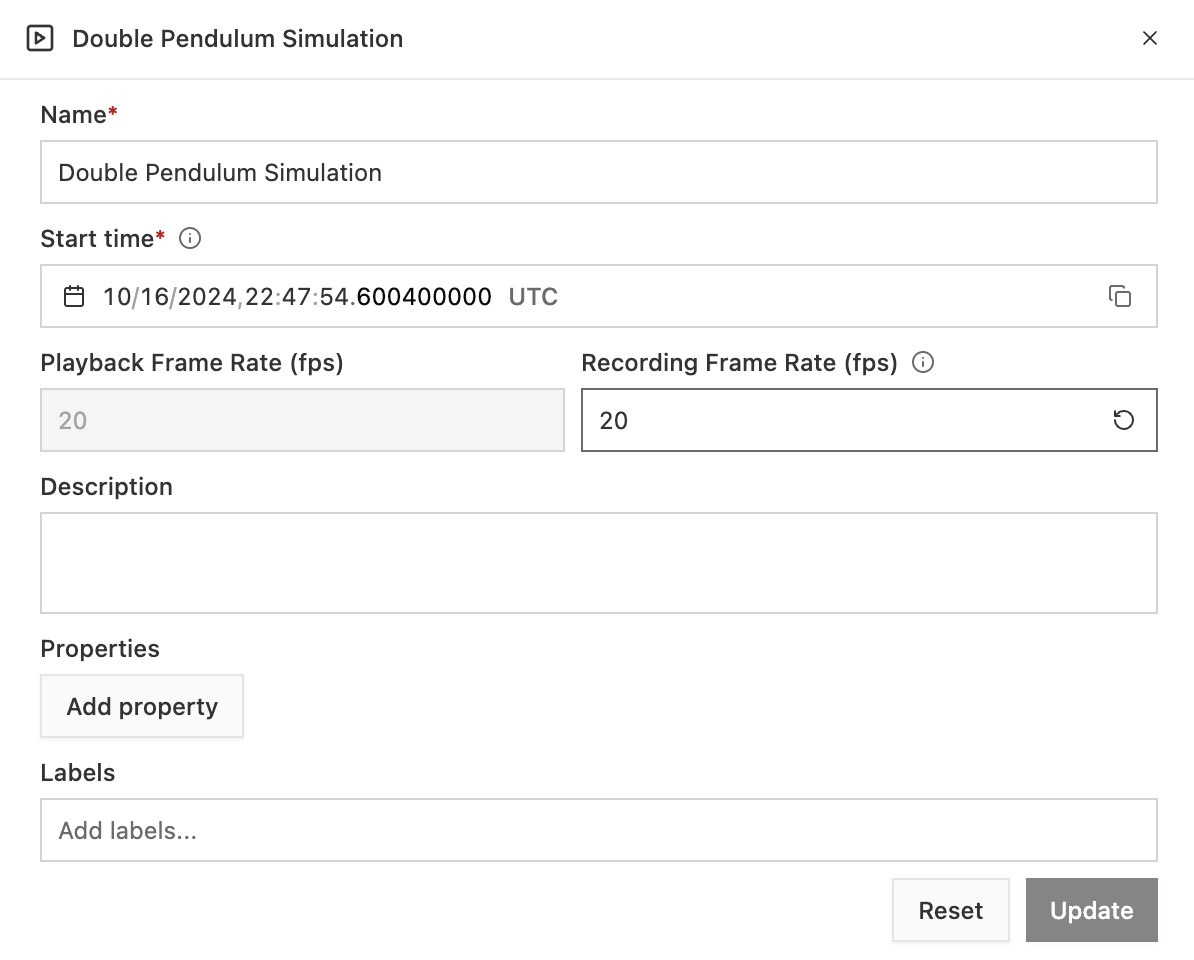
Nominal has many tools to precisely sync video playback with channel data that was either extracted from the video or recorded independently at the same time as the video.

If you select a video on the video datasets page (login required), then you can adjust video metadata such as it start timestamp.

Create a Workbook

Our simulation video and channel data is now uploaded on the Nominal platform, where it can be collaboratively analyzed and benchmarked against real-world data.

Below is an example Nominal Workbook that syncs the pendulum fulcrum heights with the pendulum simulation video playback:

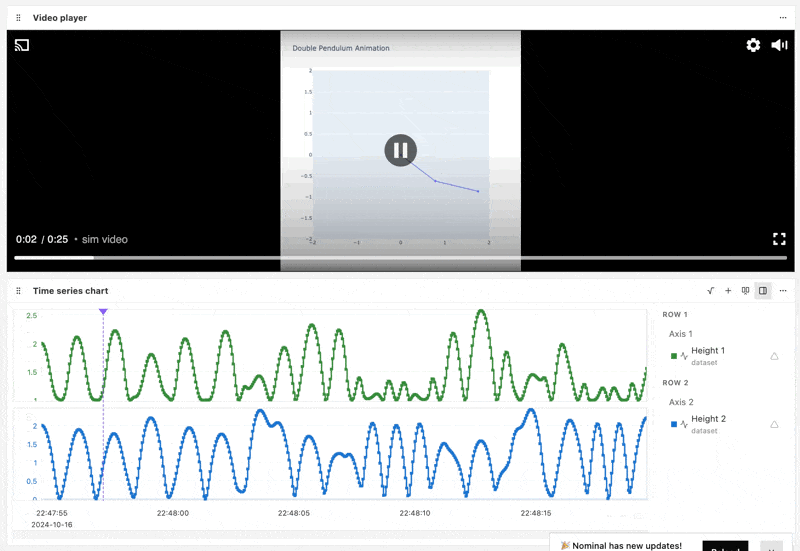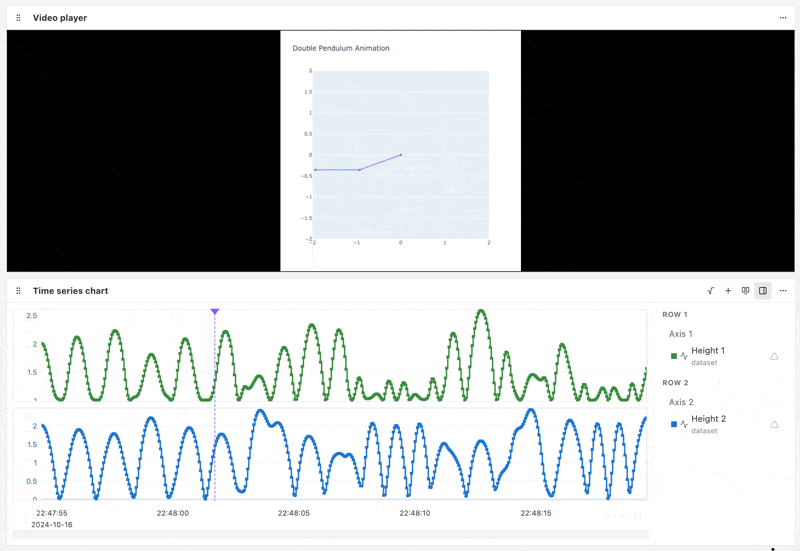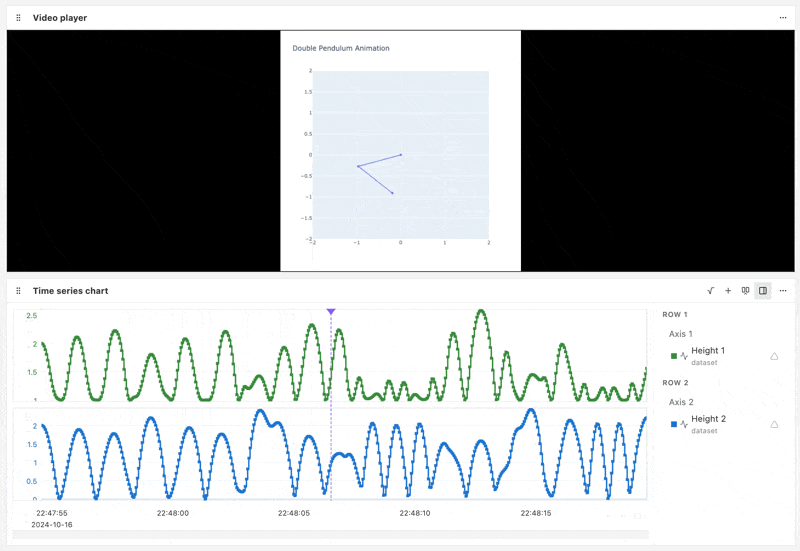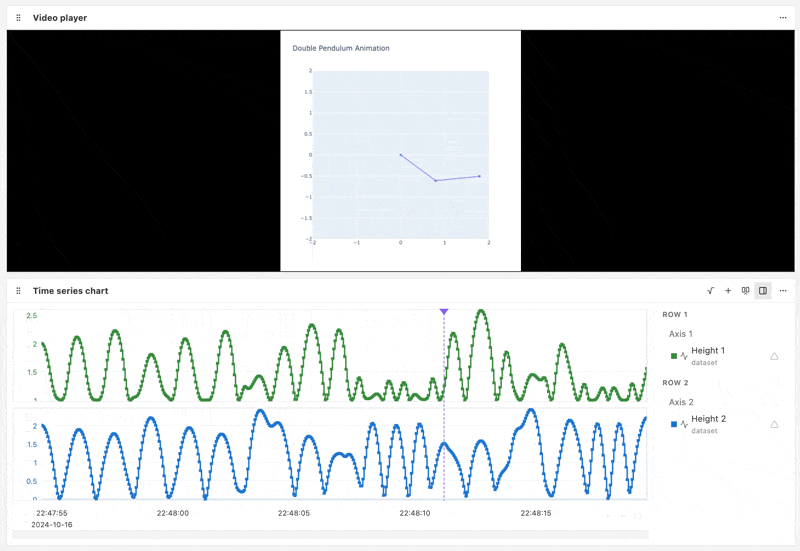
Other channels such as pendulum fulcrum momentum, acceleration, and kinetic energy can also be plotted. Workbook transforms and formulas can be used to calculate derived channels such as the RMS acceleration.

As an exercise, consider solving the simulation with a different ODE solver and comparing the results in a Nominal Workbook.

1	import numpy as np
2	import plotly.graph_objs as go
3	from scipy.integrate import solve_ivp
4
5	# Parameters for the double pendulum
6	m1, m2 = 1.0, 1.0 # masses of the pendulums
7	L1, L2 = 1.0, 1.0 # lengths of the pendulums
8	g = 9.81 # gravitational acceleration
9
10	# Equations of motion for the double pendulum
11	def double_pendulum_equations(t, y):
12	theta1, z1, theta2, z2 = y
13	delta = theta2 - theta1
14
15	# Equations of motion
16	den1 = (m1 + m2) * L1 - m2 * L1 * np.cos(delta) * np.cos(delta)
17	den2 = (L2 / L1) * den1
18
19	dydt = [
20	z1,
21	(m2 * L1 * z1 * z1 * np.sin(delta) * np.cos(delta) +
22	m2 * g * np.sin(theta2) * np.cos(delta) +
23	m2 * L2 * z2 * z2 * np.sin(delta) -
24	(m1 + m2) * g * np.sin(theta1)) / den1,
25	z2,
26	(- m2 * L2 * z2 * z2 * np.sin(delta) * np.cos(delta) +
27	(m1 + m2) * (g * np.sin(theta1) * np.cos(delta) -
28	L1 * z1 * z1 * np.sin(delta) -
29	g * np.sin(theta2))) / den2
30	]
31	return dydt
32
33	# Initial conditions and time span
34	y0 = [np.pi / 2, 0, np.pi / 2, 0] # initial angles and angular velocities
35	t_span = (0, 25)
36	t_eval = np.linspace(*t_span, 500)
37
38	# Solve the equations
39	solution = solve_ivp(double_pendulum_equations, t_span, y0, t_eval=t_eval, method='RK45')
40	theta1, theta2 = solution.y[0], solution.y[2]
41
42	# Calculate positions of the pendulums
43	x1 = L1 * np.sin(theta1)
44	y1 = -L1 * np.cos(theta1)
45	x2 = x1 + L2 * np.sin(theta2)
46	y2 = y1 - L2 * np.cos(theta2)
47
48	# Create animation using plotly
49	frames = []
50	for i in range(len(t_eval)):
51	frames.append(go.Frame(data=[
52	go.Scatter(x=[0, x1[i], x2[i]], y=[0, y1[i], y2[i]], mode="lines+markers")
53	]))
54
55	# Set up the initial plot
56	fig = go.Figure(
57	data=[go.Scatter(x=[0, x1[0], x2[0]], y=[0, y1[0], y2[0]], mode="lines+markers")],
58	layout=go.Layout(
59	title="Double Pendulum Animation",
60	xaxis=dict(range=[-2, 2], zeroline=False),
61	yaxis=dict(range=[-2, 2], zeroline=False),
62	updatemenus=[dict(type="buttons", showactive=False, buttons=[dict(label="Play",
63	method="animate",
64	args=[None, {"frame": {"duration": 50, "redraw": True},
65	"fromcurrent": True}])])],
66	width=600,
67	height=600
68	),
69	frames=frames
70	)
71
72	# Show the animation
73	fig.show()

1	import os
2	import numpy as np
3	import plotly.graph_objs as go
4	from scipy.integrate import solve_ivp
5	import imageio.v2 as imageio
6
7	# Parameters for the double pendulum
8	m1, m2 = 1.0, 1.0
9	L1, L2 = 1.0, 1.0
10	g = 9.81
11
12	# Equations of motion
13	def double_pendulum_equations(t, y):
14	theta1, z1, theta2, z2 = y
15	delta = theta2 - theta1
16
17	den1 = (m1 + m2) * L1 - m2 * L1 * np.cos(delta) ** 2
18	den2 = (L2 / L1) * den1
19
20	dydt = [
21	z1,
22	(m2 * L1 * z1 ** 2 * np.sin(delta) * np.cos(delta) +
23	m2 * g * np.sin(theta2) * np.cos(delta) +
24	m2 * L2 * z2 ** 2 * np.sin(delta) -
25	(m1 + m2) * g * np.sin(theta1)) / den1,
26	z2,
27	(- m2 * L2 * z2 ** 2 * np.sin(delta) * np.cos(delta) +
28	(m1 + m2) * (g * np.sin(theta1) * np.cos(delta) -
29	L1 * z1 ** 2 * np.sin(delta) -
30	g * np.sin(theta2))) / den2
31	]
32	return dydt
33
34	# Initial conditions and time span
35	y0 = [np.pi / 2, 0, np.pi / 2, 0]
36	t_span = (0, 25)
37	t_eval = np.linspace(*t_span, 500)
38
39	# Solve the equations
40	solution = solve_ivp(double_pendulum_equations, t_span, y0, t_eval=t_eval, method='RK45')
41	theta1, theta2 = solution.y[0], solution.y[2]
42
43	# Calculate positions
44	x1 = L1 * np.sin(theta1)
45	y1 = -L1 * np.cos(theta1)
46	x2 = x1 + L2 * np.sin(theta2)
47	y2 = y1 - L2 * np.cos(theta2)
48
49	# Save frames as images
50	filenames = []
51	for i in range(len(t_eval)):
52	fig = go.Figure(
53	data=[go.Scatter(x=[0, x1[i], x2[i]], y=[0, y1[i], y2[i]], mode="lines+markers")],
54	layout=go.Layout(
55	title="Double Pendulum Animation",
56	xaxis=dict(range=[-2, 2], zeroline=False),
57	yaxis=dict(range=[-2, 2], zeroline=False),
58	width=600,
59	height=600
60	)
61	)
62	filename = f'frame_{i:03d}.png'
63	fig.write_image(filename)
64	filenames.append(filename)
65
66	# Create video from frames using imageio
67	with imageio.get_writer('double_pendulum.mp4', fps=20) as writer:
68	for filename in filenames:
69	image = imageio.imread(filename)
70	writer.append_data(image)
71
72	# Cleanup
73	for filename in filenames:
74	os.remove(filename)
75
76	print("Video saved as 'double_pendulum.mp4'")

1	import numpy as np
2	import pandas as pd
3	from scipy.integrate import solve_ivp
4	from datetime import datetime, timedelta
5
6	# Parameters for the double pendulum
7	m1, m2 = 1.0, 1.0 # masses of the pendulums
8	L1, L2 = 1.0, 1.0 # lengths of the pendulums
9	g = 9.81 # gravitational acceleration
10
11	# Equations of motion for the double pendulum
12	def double_pendulum_equations(t, y):
13	theta1, z1, theta2, z2 = y
14	delta = theta2 - theta1
15
16	# Equations of motion
17	den1 = (m1 + m2) * L1 - m2 * L1 * np.cos(delta) * np.cos(delta)
18	den2 = (L2 / L1) * den1
19
20	dydt = [
21	z1,
22	(m2 * L1 * z1 * z1 * np.sin(delta) * np.cos(delta) +
23	m2 * g * np.sin(theta2) * np.cos(delta) +
24	m2 * L2 * z2 * z2 * np.sin(delta) -
25	(m1 + m2) * g * np.sin(theta1)) / den1,
26	z2,
27	(- m2 * L2 * z2 * z2 * np.sin(delta) * np.cos(delta) +
28	(m1 + m2) * (g * np.sin(theta1) * np.cos(delta) -
29	L1 * z1 * z1 * np.sin(delta) -
30	g * np.sin(theta2))) / den2
31	]
32	return dydt
33
34	# Initial conditions and time span
35	y0 = [np.pi / 2, 0, np.pi / 2, 0] # initial angles and angular velocities
36	t_span = (0, 25)
37	t_eval = np.linspace(*t_span, 500)
38
39	# Solve the equations
40	solution = solve_ivp(double_pendulum_equations, t_span, y0, t_eval=t_eval, method='RK45')
41	theta1, theta2 = solution.y[0], solution.y[2]
42
43	# Calculate positions, velocities, accelerations, and energies
44	x1 = L1 * np.sin(theta1)
45	y1 = -L1 * np.cos(theta1)
46	x2 = x1 + L2 * np.sin(theta2)
47	y2 = y1 - L2 * np.cos(theta2)
48
49	vx1 = np.gradient(x1, t_eval)
50	vy1 = np.gradient(y1, t_eval)
51	vx2 = np.gradient(x2, t_eval)
52	vy2 = np.gradient(y2, t_eval)
53
54	ax1 = np.gradient(vx1, t_eval)
55	ay1 = np.gradient(vy1, t_eval)
56	ax2 = np.gradient(vx2, t_eval)
57	ay2 = np.gradient(vy2, t_eval)
58
59	momentum_1_x = m1 * vx1
60	momentum_1_y = m1 * vy1
61	momentum_2_x = m2 * vx2
62	momentum_2_y = m2 * vy2
63
64	height_1 = y1 + L1 + L2
65	height_2 = y2 + L1 + L2
66
67	kinetic_energy_1 = 0.5 * m1 * (vx12 + vy12)
68	kinetic_energy_2 = 0.5 * m2 * (vx22 + vy22)
69
70	potential_energy_1 = m1 * g * (y1 + L1 + L2)
71	potential_energy_2 = m2 * g * (y2 + L1 + L2)
72
73	# Generate ISO8601 formatted timestamps
74	start_time = datetime.now()
75	absolute_time = [start_time + timedelta(seconds=t) for t in t_eval]
76
77	# Create DataFrame with full header names
78	data = {
79	"Timestamp (ISO8601)": [t.isoformat() for t in absolute_time],
80	"Momentum 1 (X)": momentum_1_x, "Momentum 1 (Y)": momentum_1_y,
81	"Momentum 2 (X)": momentum_2_x, "Momentum 2 (Y)": momentum_2_y,
82	"Acceleration 1 (X)": ax1, "Acceleration 1 (Y)": ay1,
83	"Acceleration 2 (X)": ax2, "Acceleration 2 (Y)": ay2,
84	"Velocity 1 (X)": vx1, "Velocity 1 (Y)": vy1,
85	"Velocity 2 (X)": vx2, "Velocity 2 (Y)": vy2,
86	"Height 1": height_1, "Height 2": height_2,
87	"Kinetic Energy 1": kinetic_energy_1, "Kinetic Energy 2": kinetic_energy_2,
88	"Potential Energy 1": potential_energy_1, "Potential Energy 2": potential_energy_2
89	}
90
91	df = pd.DataFrame(data)
92
93	# Save the DataFrame to a CSV file
94	csv_file_path_full_headers = "double_pendulum_full_headers.csv"
95	df.to_csv(csv_file_path_full_headers, index=False)
96
97	df

1	import nominal.nominal as nm
2
3	nm.set_token(
4	base_url = 'https://api.gov.nominal.io/api',
5	token = '* * *' # Replace with your Access Token from
6	# https://app.gov.nominal.io/settings/user?tab=tokens
7	)

1	import nominal.nominal as nm
2
3	sim_run = nm.create_run_csv(
4	file = "double_pendulum_full_headers.csv",
5	name = "double_pendulum_run",
6	timestamp_column = "Timestamp (ISO8601)",
7	timestamp_type = "iso_8601",
8	)